
Definecommand.
Define f(x,y,z,[...]) = [Function(x,y,z,[...])]
The result of Functionis returned directly to the result line.
cis(θ)
compToRect()to convert from polar to rectangular form.
Define cis(x)=cos(x)+i*sin(x) |

cis, we call this function.
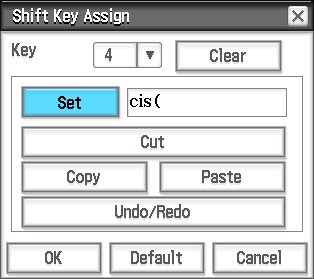
Systemtab. (you can add shift-keys for anything, even text which doesn't evaluate to a defined function.)
zroot, returns the De Moivre roots of some number, raised to the power
p, equal to the complex number
z
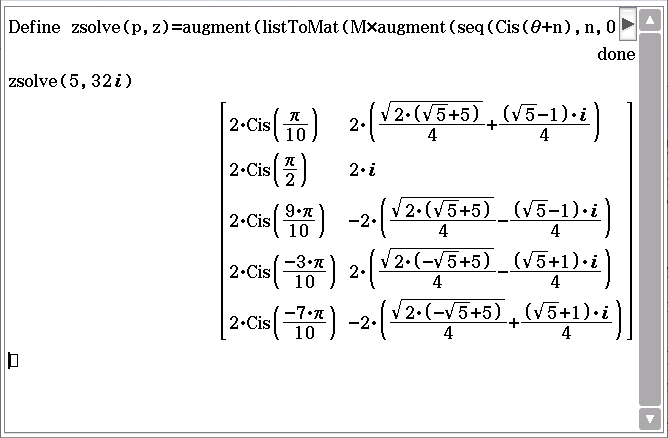
Define zsolve(p,z)=augment(listToMat(M*augment(seq(Cis(θ+n),n,0,π,d),seq(Cis(θ+n),n,-d,-π,-d))),listToMat(M*augment(seq(e^(i(θ+n)),n,0,π,d),seq(e^(i(θ+n)),n,-d,-π,-d))))|{θ=arg(z^(1/p)),M=(re(z)^2+im(z)^2)^(1/(2p)),d=2π/p} |
Define zsolve(p,z)=augment( |
|
listToMat( |
|
M*augment( |
|
seq(Cis(θ+n),n,0,π,d), |
|
seq(Cis(θ+n),n,-d,-π,-d) |
|
), |
|
), |
|
listToMat( |
|
M*augment( |
|
seq(e^(i(θ+n)),n,0,π,d), |
|
seq(e^(i(θ+n)),n,-d,-π,-d) |
|
) |
|
) |
|
)|{ |
|
θ=arg(z^(1/p)), |
|
M=(re(z)^2+im(z)^2)^(1/(2p)), |
|
d=2π/p |
|
} |
| Function walkthrough | ||
|---|---|---|
Define zsolve(p,z)=augment( | //Defines our custom command. augment() joins two arrays together (the polar and rectangular array columns) | |
listToMat( | //listToMat() converts a list (generated by seq()) to a matrix so it looks better. | |
M*augment( | //We multiply the list (below) by M, The magnitude of the zeroth solution. M is multiplied to all values in the augmented (joined) list. augment() concatenates two lists. | |
seq(Cis(θ+n),n,0,π,d), | //seq() is a function which generates a list based on a sequence. For example, seq(x^2,x,0,6,2) => {0,4,16,36}. Here we generate a list of polar coordinates with angles from 0 to π, with a constant θ added to n, a number which is generated from the seq() function. We increment each step by d, a constant. Also note the capital 'Cis' - this prevents it from being evaluated into rectangular form if cis() is defined. Cis() must be undefined to display in this form. | |
seq(Cis(θ+n),n,-d,-π,-d) | //Similar to the last line, except we increment by -d, starting at -d (to prevent a 'double up' of Cis(θ+0)) and counting to -π | |
), | //Closing bracket for augment. We augment the sequence for positive angles and negative angles into one list. | |
), | //Closing bracket for listToMat | |
listToMat( | //We repeat the process again. This time, we generate the rectangular form column. | |
M*augment( | ||
seq(e^(i(θ+n)),n,0,π,d), | //Notice how we do not use Cis(), but Euler's formula to evaluate. We can use cis(θ+n) or cos(θ+n)+i*sin(θ+n), but Euler's formula is compact and always works (unlike cis() which might not be defined) | |
seq(e^(i(θ+n)),n,-d,-π,-d) | ||
) | ||
) | ||
)|{ | //This pipe or bar character is documented as the "with" operator. For example, (2x)|{x=5} evaluates to 10. We store constants within the curly braces to make things neater to represent. | |
θ=arg(z^(1/p)), | //This gets the phase of the zeroth solution. The zeroth solution is always the pth root of z. | |
M=(re(z)^2+im(z)^2)^(1/(2p)), | //This is the magnitude. Simple stuff, we multiply the half by 1/p to skip a step (because the root is z^(1/p) => M^(1/p)) | |
d=2π/p | //This is our angle difference. Remember - you need to state this for one mark. | |
} | //Don't forget to close your brackets! tada! | |